賈尼別科夫效應
今天,來自物理學領域的一些問題: 賈尼別科夫效應也稱為網球拍定理,它解釋了具有三種不同慣性矩的旋轉物體的不穩定性。 慣性矩表示物體抵抗其旋轉運動變化的能力。 它取決於特定的旋轉軸和幾何形狀。 理解經典的哈密頓系統的動力學仍然是一個至關重要的目標,其應用遠遠超出了數學描述。 對於具有很少自由度的可集成系統,一種有效的方法是基於幾何分析來表徵機械系統的動態特性。 這種幾何現象通常是可以通過實驗觀察到的某些效果的魯棒性的起源。 其中之一就是所謂的。 賈尼別科夫效應 或也稱為網球拍效果。
賈尼別科夫效應在國際空間站失重中
可以在此處找到該現象的出色且詳盡的理論推導(https://arxiv.org/pdf/1606.08237.pdf)。 我們在這裡與一個較粗暴的人打交道,但他仍然解釋了這種現象。 不幸的是,這裡需要一些有關剛體動力學的先驗知識:
考慮具有慣性矩I1,I2和I3的慣性矩陣(對角線化),使得I1最小,I3最大。 現在考慮圍繞主慣性矩I3的軸的運動。 角速度矢量為:
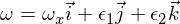
ε是其他兩個主軸上的小擾動。 如果現在將其插入到歐拉方程中,則會得到:
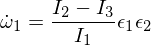
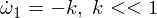
現在,我們對第二個歐拉方程進行微分:
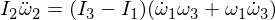
在我們的表達式中替換了Ω1和Ω3,並且由於乘以ε使它們小得足以忽略,
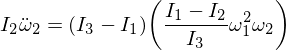
這為我們提供了Omega 2形式的微分方程:
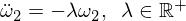
基本解決方案是:
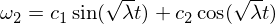
因此,我們知道omega-1軸上的旋轉紊亂是穩定的,並且會進行週期性運動,或者在剛體運動的術語中會引起進動。 Ω3障礙遵循與上述類似的論點,我將其作為練習讓您進行研究。 對於中間軸,我們有:
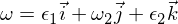
插入到歐拉方程中:
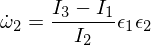
微分第三個Euler方程可得出:
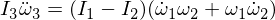
讓我們替換派生的表達式:
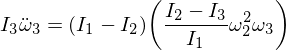
現在重新排列並推導以下微分方程:
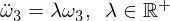
請注意,係數現在為正,因此得出指數解:
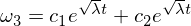
該解決方案表明,Omega 3沿中間軸不穩定,並受到Omega 2的干擾!
這是什麼意思?
現在,我們可以結合我們已經掌握和掌握的所有知識來理解該定理。 簡而言之:如果沿中間軸的旋轉受到干擾,則會生成具有指數解的微分方程。 與其他兩個軸上觀察到的精確運動相反,這導致了不穩定的運動。 這個結果非常令人驚訝。 這種定理沒有直觀的支持,因為我們無法想像中間慣性矩為何會導致旋轉不穩定。 看起來它本質上是純數學的。