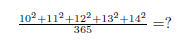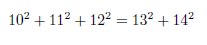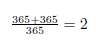代數的秘密

上一篇文章的反饋很好（感謝）。 因此，今天來自“被遺忘的數學”領域的東西-玩得開心！   

算術通常無法通過模糊的手段證明其某些優勢。 在這些情況下，我們需要更通用的代數方法。 對於這種通過代數證明是合理的算術定理，有許多用於簡化算術運算的規則。

速度倍增:

在過去沒有計算機或計算器的時代，偉大的算術家使用許多簡單的代數技巧。 使您的生活更輕鬆：

“ x”代表乘法（我們懶得嘗試LaTeX :-)）

讓我們看一下：

 988²=？

你能解決這個問題嗎？

這很簡單，讓我們仔細看看：


988 x 988 =（988 + 12）x（998 -12）+12²= 1000 x 976 + 144 = 976

也很容易了解這裡發生了什麼：

（a + b）（a-b）+b²=a²-b²+b²=a²

到目前為止還算可以。 現在，讓我們嘗試快速進行數學運算-甚至組合

986 x 997，不帶計算器！

986 x 997 =（986-3）x 1000 + 3 x 14 = 983

這裡發生了什麼？ 我們可以將這些因素寫下來：

了解更多